Kick Start 2022 Round B: Hamiltonian Tour Solution

It’s been years since I wrote about algorithms and coding contest. This blog actually was not intended for that purpose because I thought I decided to move on from CP. But when I tried joining Kickstart few days ago, I stumbled upon this unique problem.

Even though this is the least solved problem in this round, the problem itself actually not that hard. No esoteric techniques needed (like greedy, DnC, or DP), and even no complex data structure used in for this problem. I can argue that it is an example of good coding interview problem (sure, I will talk more about coding interview in another post).

Problem Description

Kick Start is one of Google annual coding tests beside Code Jam and Hash Code. But this contest is a bit different. The prizes for the top contestants are job opportunity at Google, not money.

Complete description can be viewed here. Given a N x M terrain with obstacles, each cell consists of 2x2 minicells. You start from top left corner (1,1). You have to find a way to visit each minicell exactly once and come back to initial corner, if any. You can only move into four true neighbors (no diagonal move).

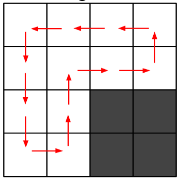
Google has released the official analysis. But I found it too difficult to understand. So, here I try to simplifying things for you guys with more intuitive way.

Preorder Traversal

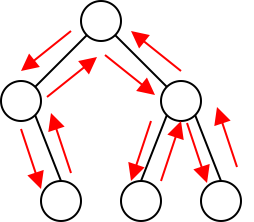
First, consider us a binary sorted tree (BST). Each node may have at most two childs, one for each side –left and right sorted in a way that left side is always less than the right side. When we want to output all elements in sorted manner increasingly, we perform what we call preorder traversal; in short left-parent-right. If we following the path of traversal, we can notice that each edge will be passed exactly twice, forward move and return move.

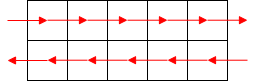
Minicell

What’s the relation of preorder traversal with this problem? The trick is in the minicell. We knew that each cell will be splitted into 2x2 minicells. Consider a path between two junctions as below. The path will then looks like a two way road. We can reduce the junction as BST node and paths between them as BST edges. Hence, the fact that each edge will be passed twice, relates with the fact that all minicells in paths will be passed exactly once.

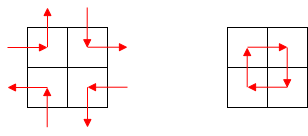
Then how about the nodes? Remember that our cells (and minicells in this matters) can connect with neighbors in four directions. For a fully connected cell, we can imagine them like a star with four inlets/outlets. In contrast, for a cell completely surrounded with obstacles, we can make a circle inside the “block”. Anything in between will follows the same rule just like a roundabout. Inlet/outlet for valid neighbors, a bypass for a blocked side. This way, all 2x2 minicells will get visited. We just need to make sure the direction is consistent. In this articles, I choose counterclockwise direction following the problem examples.

Combining Altogether

Finally we can transform our tree into grids with nodes and edges building block above in mind. The rest is building the tree using DFS traversal as usual following counterclockwise direction. It’s guaranteed for all cells that connected, we can built a complete path. So, we need to do DFS from (1,1) corner and keep the count of visited cells. If visited cells less than total of all the cells, it means there’re unreachable cells and just output IMPOSSIBLE.